Поскольку задачу радиального преобразования нужно решать для многих спектральных интервалов, либо внутри контура одной линии, либо для многих линий и (или) фона, но в то же время надо учесть, что значения ε(λ,r) для конкретного источника коррелированы, предложен алгоритм радиального преобразования [16], предполагающий коллективную обработку двумерного массива отсчетов b(λ,x), основанный на использовании описанного выше метода главных компонент. Высокая эффективность алгоритма для подавления шумов без введения какой-либо дополнительной априорной информации продемонстрирована в [16] на примере обработки результатов модельного эксперимента. Впоследствии этот метод был обобщен на случай, когда нельзя пренебречь искажающим действием спектрального прибора на каждый профиль bx(λ) [17]. В данной работе метод впервые применен к реальным экспериментальным массивам.
Автоматизированная система осуществляет сканирование по пространственной координате х - расстоянию от оси источника и для определенных положений хk (пусть их число равно m) и регистрирует распределение отсчетов фотоприемного устройства Fik, соответствующих различным длинам волн (λi) (число спектральных интервалов обозначим n).
Fi,k = q∫b(λ,xk)g(λ - λi)dλ (2.2.5)
Здесь b(λ,хk)- спектральная энергетическая яркость поверхности источника на расстоянии от оси хk, g - аппаратная функция спектрального прибора, q - коэффициент, зависящий от чувствительности фотоприемника (в главе 4 описан метод его определения), но т.к. он практически постоянен в пределах контура одной спектральной линии в дальнейшем описании алгоритма он опускается.
Вместо исключения аппаратных искажений из каждого профиля Fik при фиксированном k и радиального преобразования каждой спектральной компоненты (при фиксированном i) проводится "коллективная" обработка исходного массива, при которой существенно сокращается число операций и, главное, каждая операция совершается над распределением, полученным путем усреднения значительного числа отсчетов, что повышает устойчивость результата к шумам.
Сначала находится средний вектор отсчетов в зависимости от пространственной координаты (его компоненты усреднены по всем длинам волн):
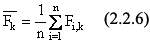
Затем вычисляется ковариационная матрица массива отсчетов:
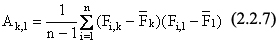Массив Fik раскладывается по собственным векторам матрицы А, причем учитываются только вектора Up, отвечающие собственным значениям матрицы А, превосходящим величину оценки дисперсии воспроизводимости одного отсчета F - SF2 (оценивается при повторных измерения одного и того же массива). Вследствие сильной корреляции отсчетов внутри массива число таких векторов v всегда существенно меньше m (для всех обработанных спектральных линий это число не превосходило 2).
Адекватность описания массива Fik моделью:
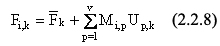может быть проверена по критерию Фишера [14].
Здесь Мi,p- проекции спектрального распределения на вектор с номером р.
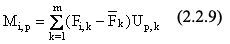и только они зависят от длин волн и из них в случае необходимости надо исключать аппаратные искажения, результат такого исключения обозначим Li,p.
Fk и Up зависят только от координат и над ними надо осуществлять радиальные преобразования (R - оператор преобразования).
В результате искомые контура в различных точках плазмы получаются согласно соотношению:
В качестве примера реализации алгоритма на рис.2.3 приведены этапы обработки массива 10 профилей одной из линий таллия (654.9нм), каждый профиль измерен в 65 спектральных точках.
При “коллективной” обработке массива вместо 65 решений интегрального уравнения свертки, оно выполнено 2 раза, а радиальное преобразование выполнено 3 раза вместо 10.
Радиальное преобразование среднего и нескольких собственных векторов Up может быть осуществлено любым корректным алгоритмом, без дополнительной регуляризации, т.к. эти распределения уже сглажены в результате усреднения по всем спектральным компонентам. В данной работе, оно осуществляется как решение системы линейных уравнений.
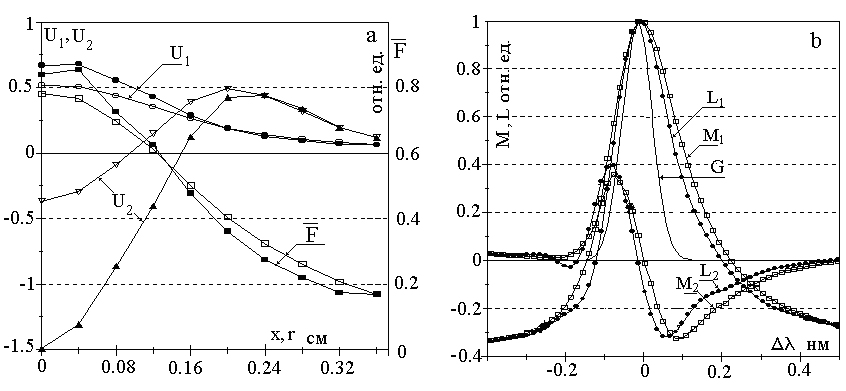
Рис.2.3. Коллективная обработка массива контуров линий таллия 654.9нм.
а - средний поперечный профиль и два первых вектора матрицы А до (светлые значки) и после (темные значки) радиального преобразования;
b - проекции контуров на собственные вектора ковариационной матрицы до исключения аппаратных искажений М1, М2 (◊) и после исключения L1,L2 (•). G - аппаратный контур,
Δλ -отсчитано от центра спектральной линии.
Эффективность коллективной обработки иллюстрируется на рисунке 2.4, на котором представлены контура коэффициентов излучения в центре разряда для наиболее слабой и, соответственно, зашумленной из исследованных линий ртути, полученные из одного массива отсчетов путем традиционной "индивидуальной" обработки (кривые 2) и путем обработки методом, описанным в главе 2 с учетом v=2 собственных векторов матрицы А (ввиду большой ширины линии аппаратные искажения здесь не исключались).
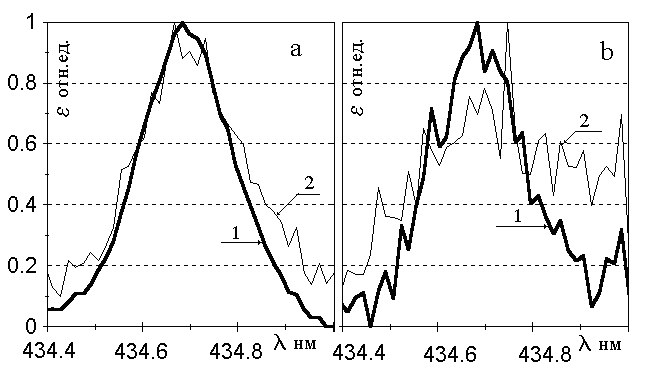
Рис. 2.4. Нормированные на максимум контура линии 434.7нм для центра разряда, полученные при обработке исходного массива различными способами, в двух фазах тока:
а) максимальная, b) минимальная интенсивность излучения.