Часто результат конкретного эксперимента выражается не одним числом, а целым набором чисел, например, при изучении радиального распределения параметров плазмы естественно поставить вопрос о влиянии условий разряда на распределение заселенности уровней. Эти распределения находят отражение в наборе экспериментальных зависимостей: яркостей В(xj) или оптических толщин B(xj), измеренных в различных точках xj и полученных в определенных условиях. Поскольку каждый отсчет τ (xj) определяется с некоторой случайной погрешностью, то решение вопроса о том, различаются ли распределения В(x), полученные для различных участков спектра или в различных условиях разряда, может быть затруднено. Особенно сложной становится задача классификации наблюдений, т.е. разбиение результатов на статистически различимые группы при большом количестве проделанных экспериментов. Для решения таких задач и применяется метод главных компонент.
Представим результат k-го эксперимента в виде набора m чисел yk1,yk2,...,ykj,...,ykm; k=1,2,...,n, где n-полное число проделанных экспериментов; j=1,2,...,m, где m-число отсчетов, полученных в одном эксперименте. Например, ykj - это яркость поверхности источника в точке, отстоящей на расстоянии хj от оси разряда, полученная в k-м эксперименте (будем считать, что во всех экспериментах яркость измеряется для одного и того же набора точек хj).
В общем случае применения метода главных компонент результат одного эксперимента называют «объектом», а отсчеты в одной экспериментальной точке «признаком», поскольку метод применяется не только к анализу массивов чисел одной размерности и одного физического смысла, но и к наборам различных характеристик объекта. Например, в биологии объектом может быть конкретное животное, а признаками - его вес, длина тела, температура, частота пульса и т.д., (но в таких случаях все характеристики должны быть выражены в относительных единицах, т.е. как отношение к некоторому значению, выбранному для данного признака за единицу, сам этот выбор не принципиален). Погрешность отсчетов в данной серии из n экспериментов будем характеризовать ковариационной матрицей D погрешностей измерения y. Эту матрицу можно построить, проделав v экспериментов для одних и тех же условий. Тогда ее элементы вычисляются по формуле (2.2.1).
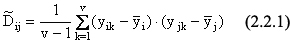Здесь i и j-номера экспериментальных точек, k-номера повторных изменений, yi(j)- средние по v измерениям в i-й (j-й) точке.
Проделаем теперь N экспериментов в различных условиях (получим N объектов). Многообразие распределений y(х), полученных во всех N экспериментах при различных условиях, характеризуется свойствами ковариационной матрицы всего массива данных, где элементы матрицы определяются по формуле:
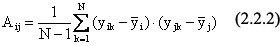Отличие от (2.2.1) состоит в том, что здесь индекс k нумерует опыты, проведенные при различных условиях, влияние которых на вид y(х) мы хотим выявить; матрица D вычисляется по распределениям y(х), полученным при постоянных условиях, т.е. ее элементы отражают воспроизводимость результатов и корреляцию между погрешностями измерений в i-й и j-й точках х.
Результаты каждого эксперимента, т.е. набор yk1,yk2,...,ykj,...,ykm можно представить точкой в m-мерном пространстве.
Вследствие наличия случайной погрешности в измерении каждая точка на самом деле «размывается» в некоторую область в том же пространстве. Если две "точки" расположены ближе, чем размер этой области "размытия", то, очевидно, результаты таких экспериментов статистически неразличим. Если в каких-то направлениях размеры "размытия" превосходят полные размеры области возможных значений y, то эти направления, очевидно, "не информативны", т.е. в этих направлениях результаты различных экспериментов вообще не различаются (на рисунке 2.2 данная ситуация иллюстрируется для простейшего случая m=2).
Области всех возможных значений y(Q1) определяютcя матрицей A, а область "размытия" - матрицей D. Матрица AD-1 определяет область возможных значений в m-мерном информационном пространстве безразмерных величин (каждое yij измеряется в единицах своей погрешности). Если хоть в каком-нибудь направлении размер этой области больше 1, значит в нашем ансамбле распределений y(x) есть статистически различимые.
Рис. 2.2. Пояснение к методу главных компонент; y1, y2 – измеряемые величины; U1,U2 - главные направления, в данном случае U2 – неинформативное направление.
Величина: V = √ λ1λ2...λv характеризует «информационный объем» эксперимента, т.е. показывает, сколько статистических различных классов есть в нашем ансамбле распределений.
Для того, чтобы разбить ансамбль на эти классы, надо найти проекции Сkp экспериментальных «точек» yk на собственные вектора Up:
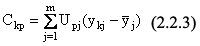здесь Upj - компоненты p-того собственного вектора матрицы AD-1 (p=1,2,...,v; j=1,2,...,m).
«Погрешность» коэффициентов оценивается по формуле:
Sср2 = UpTDUp (2.2.4)
К одному классу мы отнесем те распределения y(х), у которых все v коэффициентов Сkp неразличимы в пределах своих погрешностей.Метод может дать полезную информацию и в том случае, если матрица D неизвестна (повторные измерения при неизменных условиях не проводились). Экспериментатор может, исходя из априорных соображений, классифицировать наблюдения по проекциям только на один первый вектор (напомним, что это комбинация признаков х, по которым зависимости y(х) более всего отличаются, т.к. нахождение собственных векторов означает приведение матрицы к диагональному виду, при этом собственное значение характеризует дисперсию, т.е. разброс экспериментальных «точек» вдоль соответствующего направления).
В более сложных случаях можно использовать два и более главных направлений, если есть априорная уверенность в их значимости.