g = 8.16C62/5V3/5Naλ2/(2πc), см Δ = γ/2.8 (2.17)
Здесь Na - концентрация возмущающих атомов, V - их средняя относительная скорость, С6 - константа ван-дер-ваальсовского уширения, которая определяет изменение частоты излучения атома Δω при условии, что ближайший "сосед" находится на расстоянии R:
Δω = С6/R6, С6 = С6i - С6j (2.18)
Kонстанта С6k (k=i,j), характеризующая сдвиг k-го уровня под влиянием возмущения, рассчитывается во втором порядке теории возмущений в предположении, что атомы взаимодействуют как два диполя, и может быть представлена в виде
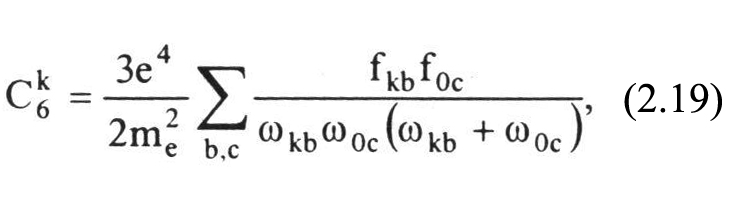где ffk - силы осцилляторов для переходов с одного из уровней данной линии (k) на все другие уровни излучающего атома, f0c - то же для переходов с основного уровня возмущающего атома на все другие уровни этого атома, ωkb, ω0c - частоты соответствующих переходов.
Условиe применимости ударного приближения имеет вид:
ω - ω0 << Ω = V6/5*C6-1/5
(2.20)
Для расстояний от центра линии, превосходящих Ω , линия имеет "статистическое крыло". Излучение в крыльях может рассматриваться как переходы между термами квазимолекулы, образованной излучающим и возмущающим атомами. Частота перехода при сближении атомов на расстоянии R
ω = [Uu(R) - Ub(R)]/ħ, (2.21)
где Uu и Ub - электронные термы квазимолекулы для верхнего (u) и нижнего (b) уровня перехода.
Переход к форме контура происходит по формуле, аналогичной (2.12), но с учетом следующих фактов.
При сильном сближении атомов нельзя не учитывать влияния их взаимодействия на взаимное расположение. При выводе формул (2.13), (2.14) положение возмущающей частицы предполагалось равновероятным в любой точке пространства. Однако чтобы подойти очень близко к излучающему атому, ей надо преодолеть его отталкивание (или наоборот, она испытывает притяжение). Поэтому в формуле для φ(ω) появляется "больцмановский фактор". В то же время экспонента не учитывается, т.к. для близких взаимодействий она очень мала, а "сворачивать" ударный и статический контур для одного и того же возмущающего процесса нельзя, т.к. они не являются независимыми. Кроме того, в выражение для φ(ω) включается суммирование по R, т.к. переходы между электронными уровнями молекулы происходят не при любых расстояниях R, а только при отвечающих принципу Франка-Кондона [12](см. рис 2.1).
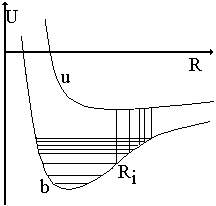
Рисунок 2.1 – Термы квазимолекулы
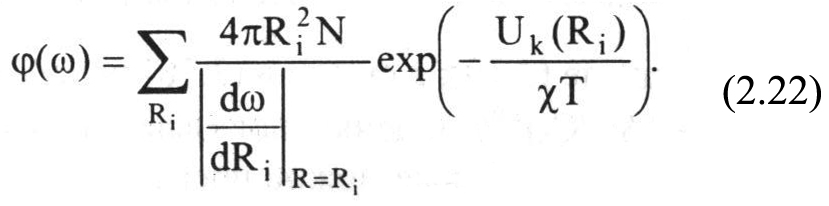Здесь k = b для контура поглощения и k = u для контура излучения, c - постоянная Больцмана, Т - температура атомов.
Такое описание предполагает, что потенциальные кривые Uu(R) и Ub(R) или хотя бы одна из них имеют минимум (только в этом случае можно говорить о дискретных "точках Кондона"). При расстояниях, отвечающих минимуму Uu(R)-Ub(R), производная в (2.22) обращается в 0, а φ(ω) - в бесконечность; реально этого не происходит, т.к. состояние с данным R длится конечное время и следует учесть его "размытие".
Из сказанного можно сделать вывод, что ван-дер-ваальсовское уширение может быть использовано в диагностических целях только в случае, если есть надежные cправочные данные о константах уширения и виде потенциалов взаимодействия. Пока же усилия, в основном, направлены на восстановление вида потенциала по форме контуров и на уточнение теории формирования контура (в частности, путем учета движения возмущающих частиц, перекрытия линий на далеких крыльях и зависимости потенциалов от температуры).