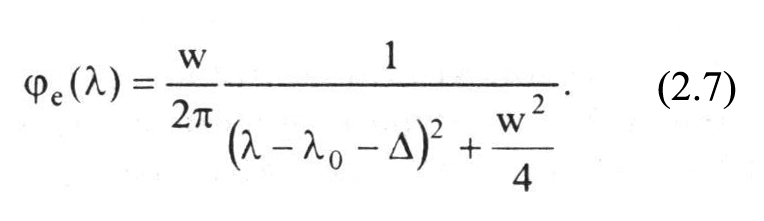Значения w и Δ пропорциональны концентрации электронов. Для многих атомных линий значения w/2 и Δ (в ангстремах) для концентрации электронов N = 1016см-3 и различных электронных температур табулированы в [9, 10] или представлены в виде зависимостей от эффективного главного квантового числа уровней и электронной температуры.
Приближенную оценку ожидаемых штарковской ширины w и сдвига Δ можно получить по формулам:
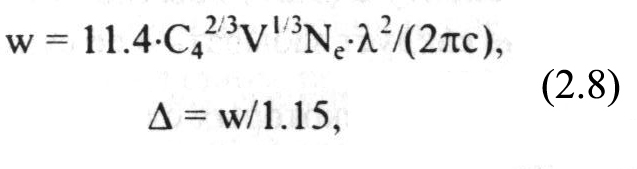где Ne - концентрация электронов (см3), V - средняя скорость электронов (см/с), С4- константа квадратичного Штарк-эффекта (в (2.8) w, λ и Δ - в см).
Для оценки С4 можно использовать приближенное выражение:
С4 = e4f/(2mħω2), (2.9)
(формула в системе CGSE, С4 - в см4с-1); здесь е, m- заряд и масса электрона, f, ω - соответственно сила осциллятора и частота перехода с верхнего уровня изучаемой линии на ближайший к нему уровень, на который возможен дипольный переход. Если нет справочных данных для величины f, то для грубой оценки ее можно положить равной 1.
Более точная оценка w получится, если учесть в С4 несколько ближайших «возмущающих» уровней, а также внести поправку на неадиабатичность столкновений с электронами.
Вклад ионов в ударную ширину невелик, т. к. их средние скорости существенно меньше, но, в целом, ионы влияют на форму контура, т. к. дают значительный вклад в статическое крыло.
В статическом приближении, которое справедливо, когда ω-ω0 >> Ω = Vi4/3*С4-1/3 (Vi - средняя скорость ионов), распределение интенсивности в линии определяется сдвигом частоты Δω, который порождает возмущающая частица, находящаяся на расстоянии R от излучающей, и вероятностью W(R)dR того, что ближайшая частица находится на расстоянии от R до R + dR.
В этом случае
Δω = С4/R4, (2.10)
причем знак сдвига определяется знаком С4, который, в свою очередь, будет положительным, если возмущающий уровень лежит ниже излучающего, и наоборот, а
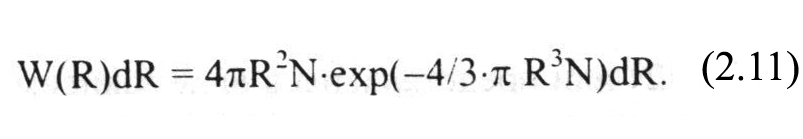(Предполагается, что N = Ni = Ne). Поскольку бинарное приближение предполагает, что среднее расстояние между частицами (N-1/3) много больше расстояния сближения частиц, которое может внести вклад в формирование контура, экспоненту в (2.11) обычно полагают равной 1. Однако в некоторых случаях не следует забывать о ее существовании.
Полагая, что φ(ω)dω = W(R)dR, (2.12)
и выражая R и dR/dω через i = Δω - ω0 с использованием (2.11). получаем форму статического контура, обусловленного влиянием ионов на линию с квадратичным Штарк-эффектом:
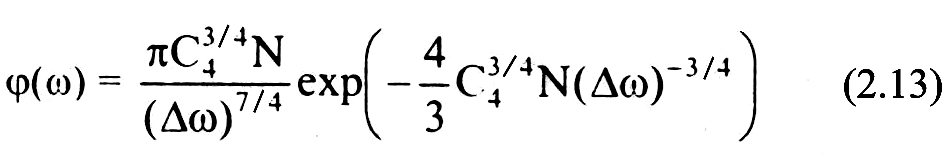или
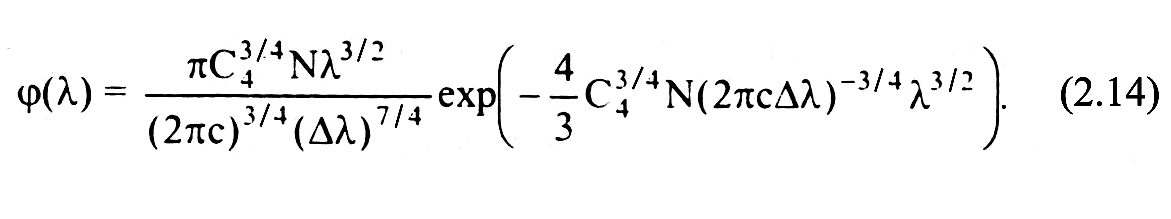В формулах (2.13, 2.14) N - в см-3 С4 - в см4с-1, с - скорость света
в см/с, Δλ = λ - λ0 - в см.
Одновременное действие электронов и ионов можно учесть, построив φ(λ) как свертку контуров, даваемых формулами (2.7) и (2.14) (при этом экспоненциальный сомножитель должен быть учтен).
Условия применимости изложенной в этом разделе модели формирования контура заключаются в том, что штарковский сдвиг должен быть меньше, чем расстояние между компонентами тонкой структуры уровня с данными значениями квантовых чисел n, 1; практически это означает, что штарковски уширенные линии мультиплетов не должны перекрываться. Нижняя граница применимости модели определяется , возможностью выделить штарковское уширение на фоне других уширяющих факторов: допплеровского уширения и влияния нейтральных частиц, которое рассматривается в следующих разделах [1].