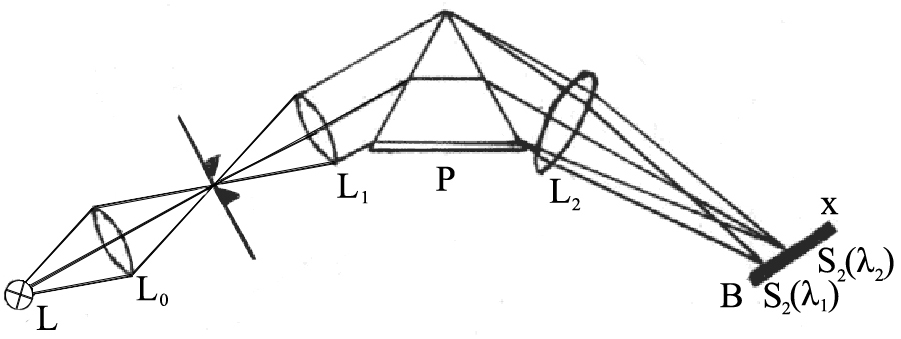
Рисунок 1.2 – Схема призменного спектрографа
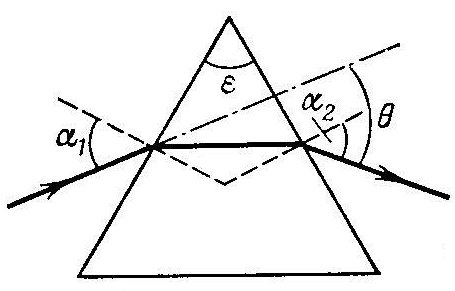
Рисунок 1.3 – Преломление света призмой в минимуме отклонения, когда α1 = α2 = α, а θ = 2α - ε
sin[(θ + ε)/2] = n sin(ε/2). (1)
Согласно (1) производная dθ/dn = 2 sin (ε/2)/cos[(θ + ε)/2] = 2 sin(ε/2) [1 — n2sin2(ε/2)]-1/2.
Следовательно, угловая дисперсия dθ/dλ = (dθ/dn) (dn/dλ) будет dθ/dλ = 2 sin(ε/2) [1 — n2sin2 (ε/2)]-1/2 dn/dλ. (2)
Это выражение показывает, что угловая дисперсия увеличивается с увеличением угла призмы ε, но не зависит от ее размеров.
Поэтому для отклонения лазерных пучков малого диаметра можно использовать маленькие призмы, не теряя при этом в угловой дисперсии. Однако в призменном спектрометре размер призмы определяет апертуру a прибора и должен быть большим для достижения большой спектральной разрешающей способности. Величина дисперсии dn/dλ зависит от материала призмы и от длины волны λ.
Разрешающая способность: λ/Δλ ≤ a(dθ/dλ).
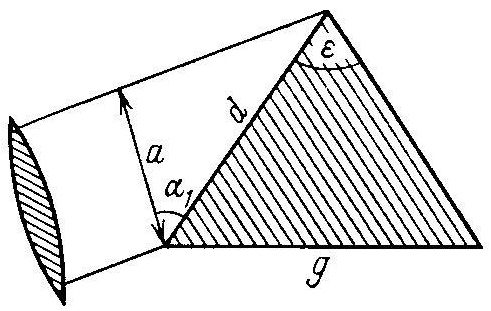
Рисунок 1.4 – Апертурная диафрагма в призменном спектрометре
Совершая подстановку получаем: λ/Δλ = g cos α1 [1 — n2sin2(ε/2)]-1/2 dn/dλ. (3)
Для минимума отклонения (1) дает n sin(ε/2) = sin(θ + ε)/2 = sin α1, и, следовательно, (3) сводится к λ/Δλ = g dn/dλ (4)
Согласно (4) теоретическая максимальная разрешающая способность зависит только от длины основания призмы g и от дисперсии материала призмы. Из-за конечной ширины щели b ≥ bmin достижимое иа практике разрешение несколько ниже, и соответствующая разрешающая способность получается не превышающей: R = λ/Δλ≤1/3 g dn/dλ.
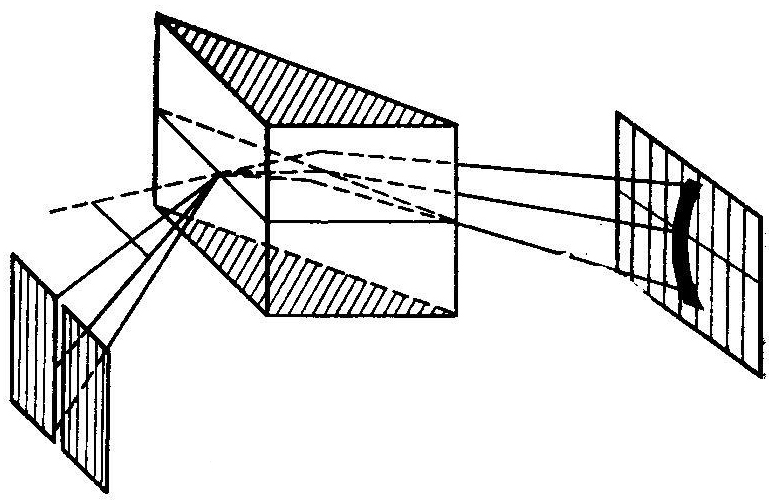
Рисунок 1.5 – Кривизна изображения щели
Если не используются ахроматические объективы (такие объективы для инфракрасной и ультрафиолетовой областей дороги), то фокусные расстояния двух объективов спектрографа уменьшаются с увеличением длины волны. Это обстоятельство можно частично компенсировать наклоном плоскости В относительно главной оси для того, чтобы поместить ее, по крайней мере примерно, в фокальную плоскость объектива L2 для диапазона больших длин волн.