Для оценки относительной высоты мобильного устройства, которое по совместительству является устройством сбора данных, могут использоваться данные двух из них: датчика атмосферного давления и акселерометра. Первый определяет величину атмосферного давления, из чего становится возможным определение относительной высоты над поверхностью земли. Второй – ускорение, произведя двойное интегрирование вертикальной компоненты которого можно определить расстояние, на которое перемещается устройство по вертикали.

Измерения акселерометра \(a_m\) помимо истинного ускорения \(a_t\), вызванного изменением скорости перемещения устройства включает в себя ускорение свободного падения \(g\) и шум. Тогда, в идеализированном случае, отбрасывая компоненту шума, измерения акселерометра в глобальной системе координат могут быть выражены следующим уравнением: $$ a_n = R_b^n \cdot a_b - g, $$ где \(R_b^n\) – матрица вращения, определяющая преобразование вектора из системы координат устройства в навигационную систему координат, \(a_b\) – измерения акселерометра в системе координат устройства.

Измерения акселерометра в системе координат устройства, однако, включают в себя ошибки, вызванные несовершенством датчика – это смещение нуля шкалы, недостоверная чувствительность, зависимость измерений от температуры и ряд других. В дальнейшем подразумевается, что на вход алгоритма подаются измерения, в которых устранены данные несовершенства датчика. Таким образом, алгоритм имеет дело с уже откалиброванными измерениями.

Информацию о высоте устройства можно получить и на основе данных об атмосферном давлении: $$ \Delta h = 44330 \cdot \left( 1 - \left(\frac{p}{p_0}\right)^{\frac{1}{5.25}}\right) - h_i, $$ где \(h_i\) – высота, определённая в момент старта или инициализации алгоритма, \(p_0\) – нормальное атмосферное давление (101325 Па).

Для объединения данных акселерометра и датчика атмосферного давления используется дискретный фильтр Калмана. Оцениваемыми параметрами являются относительная высота устройства и вертикальная скорость. Эти параметры объединены в векторе состояния системы: $$ x_k = \left[ \begin{array}{c} h \\ v_h \end{array} \right]. $$

Переходная матрица состояния этапа экстраполяции имеет следующий вид: $$ F_k = \left[ \begin{array}{cc} 1 & dt \\ 0 & 1 \end{array} \right], $$ где \(dt\) – время, прошедшее с момента предыдущего этапа обновления вектора состояния \(x_{k-1}\).

Измерения вертикального ускорения без учета ускорения свободного падения являются одноэлементным вектором управляющих воздействий, где матрица управления \(B_k\), прикладывающаяся к нему, вырождается в двухэлементный вектор: $$ B_k = \left[ \begin{array}{c} \frac{1}{2} a_t ~dt^2 \\ a_t~dt\end{array} \right], $$ где \(a_t\) – вертикальное ускорение на текущем временном интервале.

Полный этап экстраполяции для используемого фильтра Калмана состоит из прогнозирования нового вектора состояния системы и обновления ковариационной матрицы для экстраполированного вектора состояния: $$ \hat{x}_k = F_k \hat{x}_{k-1} + B_k a_t, $$ $$ P_k = F_k P_{k-1} F_k^T + Q_k, $$ где \(P_k\) – ковариационная матрица ошибок, \(Q_k\) – ковариационная матрица процесса, зависящая от периода сэмплирования датчика и параметров шумов процесса системы: $$ Q_k = \left[ \begin{array}{cc} dt^2 & 0 \\ 0 & dt^2 \end{array} \right] \mathrm{diag}([\sigma_h, \sigma_v]), $$ где \(\sigma_h\) и \(\sigma_v\) – шумы процесса, связанные с определением высоты и вертикальной скорости, которые должны быть определены экспериментально, diag() – генерация диагональной матрицы на основании вектора. Использование вертикального ускорения в качестве управляющего вектора позволяет напрямую воздействовать на состояние фильтра и уменьшить задержку в обновлении состояния системы. Это является логичным, так как измерения акселерометра необходимы для отслеживания высокодинамичного изменения высоты.

На этапе коррекции вектор измерений состоит только из одного значения высоты \(h_t\), полученного из измерения давления в момент времени \(t\). На этапе коррекции рассчитывается величина отклонения полученного на предыдущем шаге состояния системы от измеряемой величины: $$ y = h_t - H \hat{x}_{k}, $$ где \(H = [1 \quad 0].\)

Затем, согласно фильтру Калмана, рассчитывается ковариационная матрица для вектора ошибки. В данном случае, при векторе измерений единичной длины она равняется условной дисперсии: $$ S_k = P_k(1,1) + R_k, $$ где \(R_k\) – шум измерения высоты (напрямую зависит от шума измерений датчика атмосферного давления). Используя значение условной дисперсии, матрицу измерений и ковариацинную матрицу, можно рассчитать коэффициенты усиления: $$ K_k = P_k H^T \frac{1}{S_k}. $$

После этого корректируется ранее полученный вектор состояния системы: $$ \hat{x_k} = \hat{x}_{k-1} + K_k y $$ и производится перерасчет ковариационной матрицы оценки вектора состояния системы $$ P_k = (I - K_k H)P_k. $$

Для проверки эффективности работы предложенного алгоритма определения высоты устройства была проведена серия модельных и оценочных экспериментов, имитирующая различные условия использования устройства и его перемещения в помещениях.

Эксперимент 1 – состояние покоя. Устройство было стационарно, какое-либо перемещение отсутствовало. Целью данного эксперимента являлась оценка эффективности подавления шума измерений датчика атмосферного давления с помощью измерений акселерометра.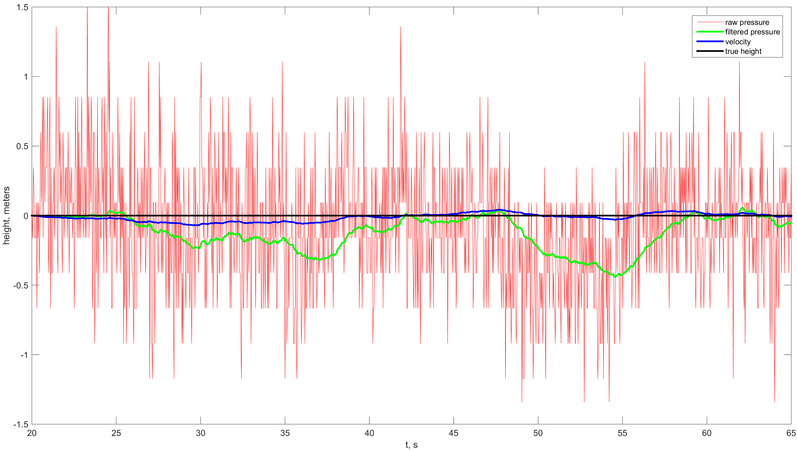

Рис.1. Графики давления и высоты в состоянии покоя.
Красный – измеренное давление, зелёный – оценённое значение высоты при помощи предложенного алгоритма, синий – вертикальная скорость, чёрный – истинная высота во время всего времени проведения эксперимента.

Эксперимент 2 – режим свободного падения. Устройство в данном эксперименте падало с заранее известной высоты (1.25 м) на мягкий матрас. Во время движения устройство могло испытывать вращение. Изначально устройство находилось на матрасе (фаза 1), затем в течение 12 с поднималось на высоту 1.25 м (фаза 2), в течение 10 с было статично (фаза 3), а затем отпускалось и падало на матрас (фаза 4). После этого вновь оставалось неподвижно (фаза 5).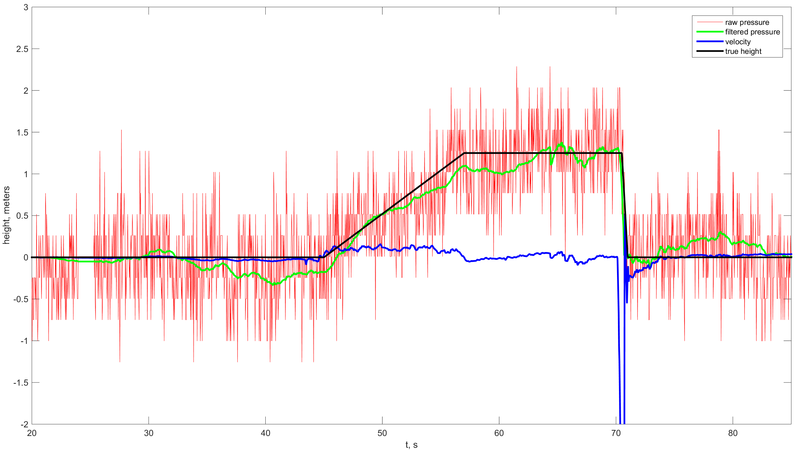

Рис.2. Графики давления и высоты в эксперименте 2 (падение).
Красный – измеренное давление, зелёный – оценённое значение высоты при помощи предложенного алгоритма, синий – вертикальная скорость, чёрный – истинная высота во время всего времени проведения эксперимента.

Эксперимент 3 – подъём и спуск по ступенькам. Устройство последовательно перемещалось два раза на 0.33 м вверх, а затем обратно вниз.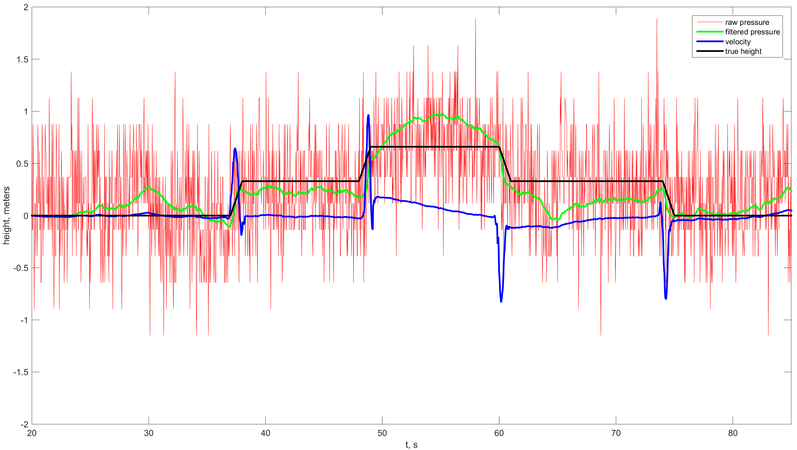

Рис.3. Графики давления и высоты в эксперименте 3 (подъём и спуск по ступенькам).
Красный – измеренное давление, зелёный – оценённое значение высоты при помощи предложенного алгоритма, синий – вертикальная скорость, чёрный – истинная высота во время всего времени проведения эксперимента.

Эксперимент 4 – движение внутри помещения. Устройство сбора данных размещалось в кармане экспериментатора. После этого экспериментатор спускался с четвертого на первый этаж.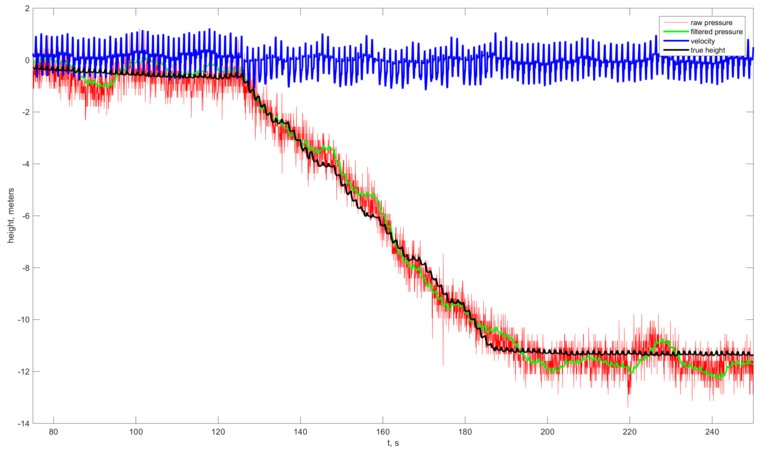

Рис.4. Графики давления и высоты в эксперименте 4 (спуск по лестнице).
Красный – измеренное давление, зелёный – оценённое значение высоты при помощи предложенного алгоритма, синий – вертикальная скорость, чёрный – истинная высота во время всего времени проведения эксперимента.

Для всех экспериментов суммарно была рассчитана кумулятивная функция ошибки в определении относительной высоты. Заметно, что естественные флуктуации величины атмосферного давления оказывают сильное влияние на итоговую оценку высоты. Их, однако, удаётся сгладить данными акселерометра и сильно уменьшить величину шума, сохраняя при этом высокую динамичность всей системы в целом.

Для всех проведённых экспериментов значение ошибки при определении относительной высоты не превышало 0.3 м в 90 % случаев.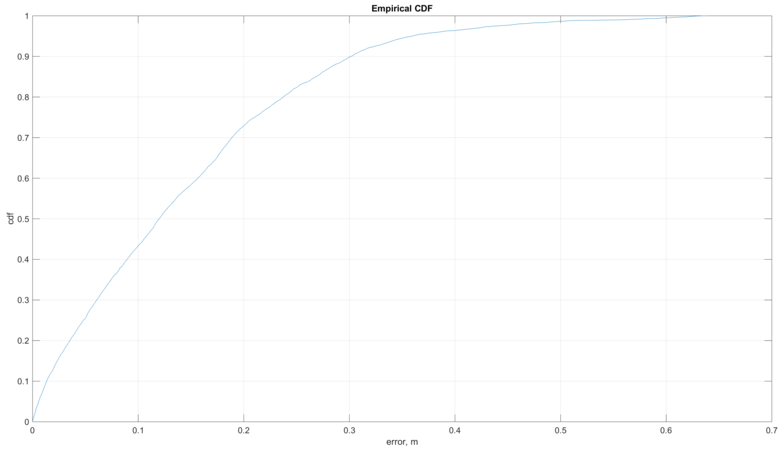

Рис.5. Кумулятивная функция ошибки.

Lab127 © По всем вопросам обращаться к Мощевикину Алексею Петровичу

Использование материалов сайта без разрешения запрещено!