Для определения высоты мобильного устройства можно использовать показания встроенного датчика атмосферного давления. Показания давления \(p\) изменяются в зависимости от высоты \(h\) над поверхностью земли. Данная зависимость описывается следующим уравнением: $$ p = p_0 e^{-\frac{Mg}{RT}h}. $$ Здесь \(p_0\) – давление на уровне моря, \(M\), \(g\), \(R\) – физические константы, \(T\) – температура воздуха (в Кельвинах).

Для простоты можно считать, что на высотах близких к уровню моря показание датчика давления линейно зависит от высоты устройства: $$ p_t = k \cdot h_t + p_0. $$

Таким образом, зная изменение значения датчика давления \(p_1\) и \(p_2\) за два последовательных момента времени \(t_1\) и \(t_2\), можно оценить изменение высоты \(\triangle h\) мобильного устройства: $$ \triangle h = h_2 - h_1 = \frac{-(p_2 - p_1)}{k}. $$

Существует несколько типов ошибок, влияющих на данные датчика атмосферного давления. Основной компонентой является шум самого датчика. Такой шум может быть смоделирован случайной величиной \(\delta p\), распределённой нормально с нулевым математическим ожиданием и заданной дисперсией \(\sigma_p\).

Для оценки величины давления по результатам зашумлённых наблюдений можно использовать фильтр Калмана.

Наблюдаемым параметром в описываемой системе является измерение атмосферного давления датчиком мобильного устройства в момент времени \(t\): \( p_t = p_h + \delta p + s, \) где \(p_h\) – истинное значение атмосферного давления на высоте \(h\), \(s\) – стационарная величина смещения в показаниях, заданная при производстве датчика.

В качестве оцениваемого параметра будем использовать величину \( x_t = p_h + s, \) равную сумме истинного атмосферного давления на высоте \(h\) и стационарного аппаратного смещения \(s\).

Поскольку информация о характере движения отсутствует, состояние системы будет характеризоваться только двумя параметрами: оценкой давления \(x_t\) и дисперсией оценки \({\sigma^2_x}_t\).

Необходимо отметить, что поскольку уравнения динамики системы не учитывают скорость изменения давления и другие параметры, вся неопределённость, связанная с возможными изменениями в системе, закладывается в параметр шумов. Для учёта возможного перемещения значение параметра шумов можно задавать в зависимости от интервала времени между измерениями. Так, внутри здания, перемещение человека по вертикали может осуществляться по лестнице, на лифте или на эскалаторе. Такие перемещения имеют определённую максимальную скорость, которая составляет 1–2 м/с.

Вектор измерений состоит только из одного значения давления \(p_t\), измеренного в момент времени \(t\). Каждое измерение характеризуется дисперсией шумов измерений \(\sigma^2_r\).

Скорректированные значения оцениваемого параметра и оценки соответствующей дисперсии вычисляются с использованием стандартных уравнений фильтра Калмана: $$ x_t = x^-_t + k_t(p_t - x^-_t), $$ $$ k_t = \frac{{\sigma^2_x}^-_t}{{\sigma^2_x}^-_t + \sigma^2_r}, $$ $$ {\sigma^2_x}_t = (1 - k_t){\sigma^2_x}^-_t. $$ Здесь символ "\(^{-}\)" означает "спрогнозированное значение".

Предложенный алгоритм является рекурсивным. Для его работы на первом этапе необходимо задать начальные значения оцениваемого параметра \(x_0\) и дисперсии \({\sigma^2_x}_0\). В данной работе величина \(x_0\) равна первому измеренному значению давления \(p_0\), а величина \({\sigma^2_x}_0\) задаётся равной дисперсии шумов измерений \(\sigma^2_r\).

Для определения эффективности разработанного алгоритма определения относительной высоты мобильного устройства были проведены модельные эксперименты, имитирующие возможные перемещения устройства внутри помещения. Для всех экспериментов максимальная вертикальная скорость объекта \(v\), задаваемая в алгоритме, составляла 1 м/с. Дисперсия шумов измерений \(\sigma_r\) задавалась равной 5 Па.

В первом эксперименте (A) предполагалось, что мобильное устройство последовательно перемещалось на следующие высоты: 0.0, 0.5, 0.0, 1.0, 0.0, 1.5, 0.0, 2.0, 0.0, 2.5 м. Время нахождения устройства на каждой высоте равнялось 20 с. Время перемещения составляло 1 с.

Во втором эксперименте (B) имитировался подъём и спуск по лестнице. Предполагалось, что человек с мобильным устройством последовательно перемещался с первого на пятый этаж, а затем спускался с пятого на первый, задерживаясь на каждом этаже определённый промежуток времени. Высота каждого этажа задавалась равной 3 м.

В третьем эксперименте (С) имитировался подъём и спуск на лифте между первым и пятым этажом. Между моментами спуска и подъёма человек с мобильным устройством задерживался на некоторое время на пятом этаже. Интервал времени между измерениями составлял 1 с.

На рисунке ниже представлены результаты экспериментов по определению относительной высоты мобильного устройства по зашумлённым измерениям давления с использованием разработанного алгоритма. Для всех трёх экспериментов представлены графики зависимости измеренного давления, истинной и посчитанной высоты от времени. Справа внизу приведен рисунок с кумулятивными функциями ошибки в определении относительной высоты.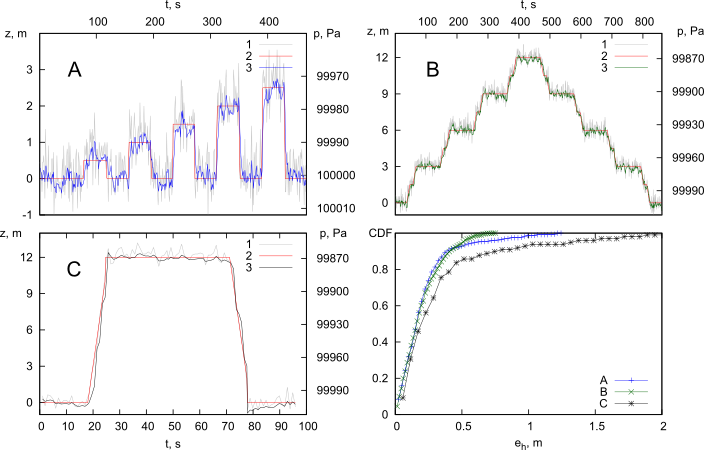

Рис.1. Результаты эксперимента по определению относительной высоты устройства.
1 – график измеренного давления, 2 – истинная высота мобильного устройства, 3 – высота, определенная алгоритмом.

Для всех рассмотренных вариантов значение ошибки в определении относительной высоты не превышало 1 м в 90 % случаев.

Разработанный алгоритм подразумевает, что определение изменения высоты на заданную величину может происходить с задержкой по времени. Для оценки величины задержки был проведен модельный эксперимент, в котором высота мобильного устройства периодически менялась от 0 до 2 м. Время нахождения устройства на одной высоте составляло 40 с. Время изменения высоты равнялось 2.5 с. Графики изменения истинной и рассчитанной высоты, а также график давления, соответствующего данному изменению представлен на рисунке ниже.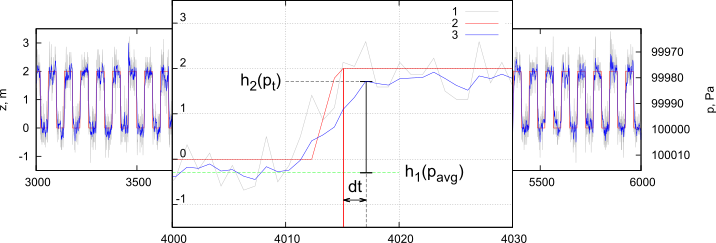

Рис.2. Эксперимент по оценке задержки в определении изменения высоты на 2 м.
1 – график измеренного давления, 2 – истинная высота мобильного устройства, 3 – высота, определенная алгоритмом.

Величина задержки вычислялась следующим образом: по серии измерений, зарегистрированных в моменты времени нахождения объекта на одной высоте, определялось среднее значение давления \(p_{avg}\) и оценка стандартного отклонения \(\sigma_{p_{avg}}\). После перемещения объекта на следующую фиксированную высоту, отличающуюся от предыдущей на величину порогового значения \(d = 2\) м, фиксировались новые измерения давления \(p_t\) (пороговое значение разницы давлений, соответствующее обозначенной высоте, рассчитывается как \(k \cdot d\)). Событие о переходе устройства на новую высоту фиксировалось, как только разница между средним значением \(p_{avg}\), соответствующим нахождению объекта на высоте \(h_1(p_{avg})\), и одним из новых измерений \(p_t\), соответствующих нахождению объекта на высоте \(h_2(p_t)\), отличалась от порогового значения разницы давлений \(k \cdot d\) менее чем на величину стандартного отклонения \(\sigma_{p_{avg}}\): $$ k \cdot d - \sigma_{p_{avg}} < |p_{avg} - p_t| < k \cdot d + \sigma_{p_{avg}}. $$

Кумулятивная функция ошибки в измерении высоты и гистограмма временной задержки в определении высоты для описанного эксперимента представлены на рисунке ниже.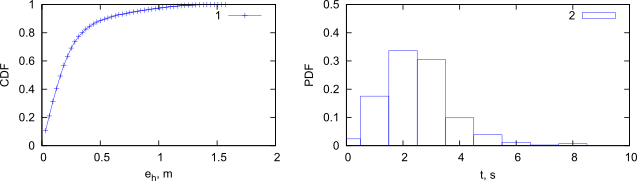

Рис.3. Результаты эксперимента по определению временной задержки в определении высоты.
1 – кумулятивная функция ошибки в определении высоты, 2 – гистограмма временной задержки.

Для приведённого эксперимента ошибка в определении относительной высоты не превышает 1 м в 90 % случаев. Наиболее вероятное значение задержки в определении относительного изменения высоты на 2 м составляет 2 с. При этом максимальная задержка по времени составляет 8 с.

Lab127 © По всем вопросам обращаться к Мощевикину Алексею Петровичу

Использование материалов сайта без разрешения запрещено!